كيف يؤثر حجم العينة على الدقة المطلوبة للقياس؟ حسّن جودة بياناتك

باختصار، لا يغير حجم العينة الأكبر الدقة المتأصلة لجهاز القياس الخاص بك، ولكنه يزيد بشكل كبير من دقة الاستنتاجات التي يمكنك استخلاصها من بياناتك. من خلال جمع المزيد من العينات، فإنك تقلل "خطأ أخذ العينات"، وهو عدم اليقين الذي يأتي من ملاحظة جزء من مجموعة بدلاً من الكل. وهذا يعني أن نتائجك من المرجح أن تكون تمثيلاً حقيقياً للسكان بأكملهم.

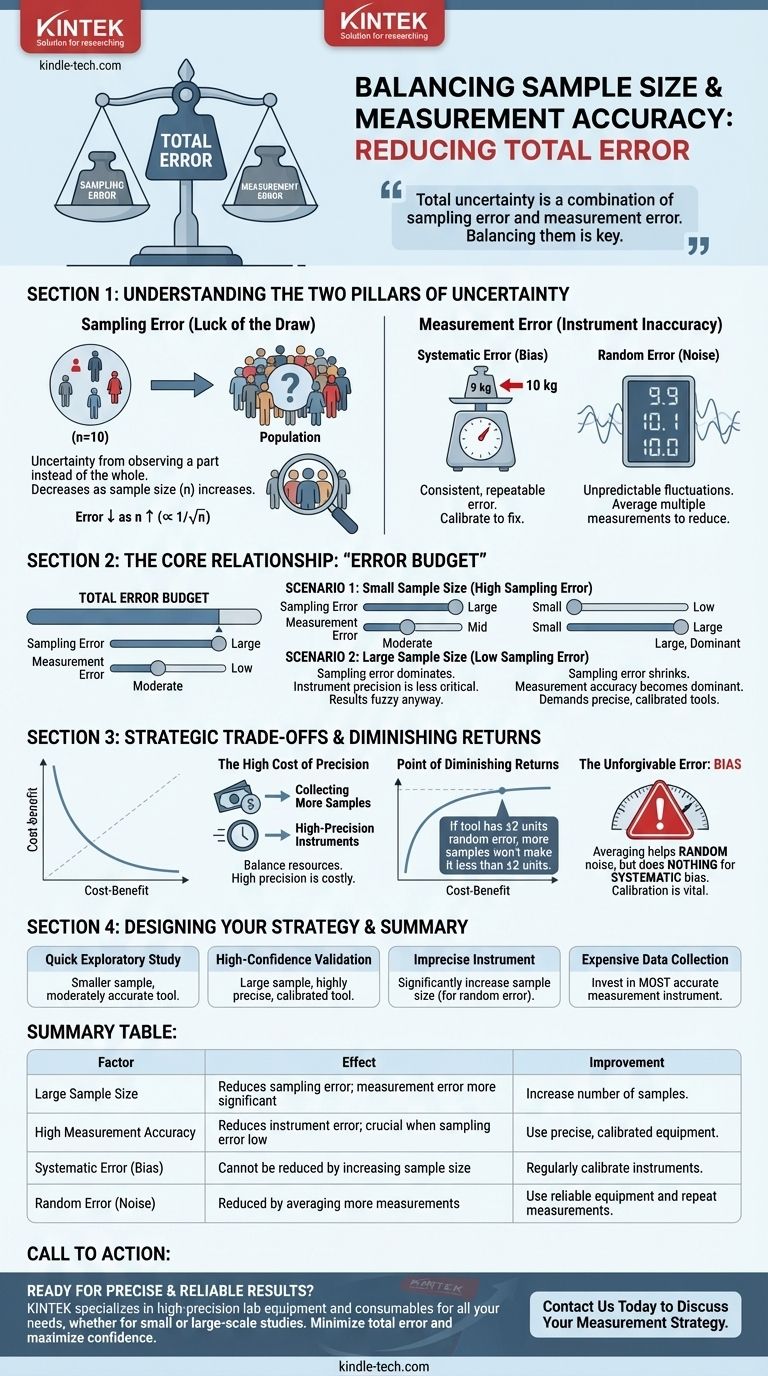
القضية الأساسية لا تتعلق فقط بحجم العينة؛ بل تتعلق بالموازنة بين مصدرين متميزين للخطأ. إجمالي عدم اليقين لديك هو مزيج من خطأ أخذ العينات (من حجم عينتك) وخطأ القياس (من جودة أداتك). فهم كيفية تفاعل هذين الأمرين هو المفتاح لتصميم دراسة فعالة.

الركيزتان الأساسيتان لعدم اليقين: أخذ العينات مقابل القياس

لفهم العلاقة بشكل كامل، يجب عليك التمييز بين النوعين الأساسيين من الأخطاء التي يمكن أن تؤثر على نتائجك. إنهما ليسا قابلين للتبادل.

فهم خطأ أخذ العينات

خطأ أخذ العينات هو "حظ القرعة". إنه الفرق العشوائي بين خصائص عينتك وخصائص السكان بأكملهم التي من المفترض أن تمثلها.

تخيل محاولة تحديد متوسط طول جميع الأشخاص في مدينة عن طريق قياس 10 أفراد فقط. قد تختار عن طريق الخطأ مجموعة طويلة أو قصيرة بشكل غير عادي.

هذا الخطأ ليس خطأ؛ إنه حقيقة إحصائية. والخبر السار هو أنه يمكن التنبؤ به ويمكن التحكم فيه. مع زيادة حجم عينتك (ن)، ينخفض خطأ أخذ العينات لديك بمعدل يتناسب مع الجذر التربيعي لحجم العينة (1/√ن). من المرجح أن تعكس العينة الأكبر السكان الحقيقيين.

فهم خطأ القياس

خطأ القياس هو عدم الدقة المتأصلة في جهاز أو طريقة القياس الخاصة بك. لا علاقة له بعدد العينات التي تأخذها.

يأتي هذا الخطأ في شكلين:

الخطأ المنهجي (التحيز): خطأ ثابت ومتكرر. فكر في ميزان يقرأ دائماً 1 كجم أعلى من الوزن الحقيقي. أخذ المزيد من القياسات لن يصلح هذا؛ ستحصل فقط على إجابة دقيقة جداً، ولكنها خاطئة.
الخطأ العشوائي (الضوضاء): تقلبات غير متوقعة في القياس. فكر في ميزان رقمي تومض آخر خانة فيه قليلاً.

يمكن أن يساعد متوسط العديد من القياسات في تقليل تأثير الخطأ العشوائي، ولكنه لا يمكن أبداً تصحيح الخطأ المنهجي. تحدد دقة أداتك حداً صارماً للحقيقة المطلقة لبياناتك.

كيف يتفاعل حجم العينة ودقة القياس

الرؤية الحاسمة هي أن هذين الخطأين يساهمان في "ميزانية الخطأ" الإجمالية لديك. هدفك هو تقليل إجمالي الخطأ، وكيفية تخصيص الموارد لمكافحة كل نوع من الأخطاء يعتمد على وضعك.

العلاقة الأساسية: "ميزانية الخطأ" الخاصة بك

فكر في مستوى الثقة المطلوب كميزانية للخطأ الكلي. أنت "تنفق" هذه الميزانية على مزيج من خطأ أخذ العينات وخطأ القياس.

إذا كان أحد مصادر الخطأ كبيراً جداً، فسوف يهيمن على نتائجك، وقد يكون لتقليل المصدر الآخر تأثير عملي ضئيل.

السيناريو 1: حجم عينة صغير

عندما يكون حجم عينتك صغيراً، يكون خطأ أخذ العينات مرتفعاً. وهو دائماً تقريباً أكبر مساهم في إجمالي عدم اليقين لديك.

في هذه الحالة، تكون دقة أداة القياس الخاصة بك أقل أهمية. ستكون نتيجتك غير واضحة على أي حال بسبب "حظ القرعة" في أخذ العينات، لذا فإن كمية صغيرة من خطأ القياس لن تجعل الصورة العامة أسوأ بكثير.

السيناريو 2: حجم عينة كبير

مع زيادة حجم عينتك، يتقلص خطأ أخذ العينات بشكل كبير. يقترب متوسط عينتك أكثر فأكثر من متوسط السكان الحقيقي.

هنا يصبح سؤال المستخدم ذا بصيرة خاصة. حجم العينة الكبير يزيد بشكل فعال من الطلب على القياس الدقيق. مع اختفاء خطأ أخذ العينات، يصبح أي خطأ من جهازك هو المصدر المهيمن لعدم اليقين.

إذا كان جهاز القياس الخاص بك يحتوي على تحيز منهجي، فإن حجم العينة الكبير سيمنحك فقط تقديراً دقيقاً جداً للقيمة الخاطئة. إنه يضخم أهمية وجود جهاز معاير ودقيق.

فهم المقايضات

يعد اتخاذ قرار بشأن حجم العينة وجودة الجهاز بمثابة موازنة استراتيجية، وغالباً ما تمليها القيود الزمنية والمالية.

التكلفة العالية للدقة

يتطلب جمع المزيد من العينات وقتاً وموارد. وبالمثل، فإن الأجهزة عالية الدقة والمعايرة بشكل مثالي باهظة الثمن. يجب أن تقرر أين تستثمر.

إن إهدار المال في حجم عينة ضخم هو إهدار إذا كانت نتائجك مقيدة في النهاية بأداة قياس رخيصة وغير دقيقة.

نقطة التناقص الغلة

هناك نقطة لا يؤدي فيها زيادة حجم العينة إلى أي فائدة تقريباً. إذا كان لأداة القياس الخاصة بك خطأ عشوائي متأصل يبلغ ±2 وحدة، فلا يمكنك أبداً تحقيق فاصل ثقة نهائي أصغر من ذلك، بغض النظر عن عدد العينات التي تأخذها.

وبالمثل، فإن شراء جهاز بملايين الدولارات لا معنى له إذا كنت تخطط لأخذ ثلاث عينات فقط، حيث سيتجاوز خطأ أخذ العينات الهائل لديك الدقة المذهلة للجهاز.

الخطأ الذي لا يغتفر: التحيز

تذكر أن زيادة حجم العينة تساعد في متوسط الضوضاء العشوائية ولكنها لا تفعل شيئاً على الإطلاق لإصلاح التحيز المنهجي.

غالباً ما تكون معايرة أجهزتك للقضاء على الخطأ المنهجي هي أهم خطوة يمكنك اتخاذها لضمان سلامة بياناتك، بغض النظر عن حجم العينة.

تصميم استراتيجية القياس الخاصة بك

لا يوجد حجم عينة "صحيح" واحد أو مستوى دقة واحد. يعتمد الاختيار الصحيح كلياً على هدفك وقيودك.

إذا كان تركيزك الأساسي هو دراسة استكشافية سريعة: قد يكون حجم العينة الأصغر المقترن بجهاز دقيق إلى حد ما كافياً لتحديد الاتجاهات الرئيسية وتوجيه البحث المستقبلي.
إذا كان تركيزك الأساسي هو التحقق عالي الثقة (على سبيل المثال، الموافقة التنظيمية): تحتاج إلى عينة كبيرة ومختارة بعناية وجهاز دقيق ومعاير للغاية لتقليل كل من خطأ أخذ العينات وخطأ القياس إلى درجة يمكن التحقق منها.
إذا كان جهاز القياس الخاص بك معروفاً بأنه غير دقيق: يمكنك التعويض عن طريق زيادة حجم عينتك بشكل كبير، ولكن فقط إذا كان الخطأ عشوائياً، وليس منهجياً. سيؤدي ذلك إلى تقليل عدم اليقين الإجمالي لديك، ولكن فقط حتى الحد الذي تحدده عيوب الجهاز.
إذا كان جمع العينات مكلفاً للغاية أو صعباً (على سبيل المثال، استكشاف الفضاء): يجب عليك الاستثمار في أدق جهاز قياس ممكن لاستخراج أقصى قيمة من كل نقطة بيانات ثمينة.

في النهاية، تتعلق الموازنة بين حجم العينة ودقة القياس بتخصيص مواردك بشكل استراتيجي لمكافحة أهم مصادر عدم اليقين في سياقك المحدد.

جدول الملخص:

العامل	التأثير على النتائج	كيفية التحسين
حجم عينة كبير	يقلل من خطأ أخذ العينات؛ يجعل خطأ القياس أكثر أهمية.	زيادة عدد العينات المقاسة.
دقة قياس عالية	يقلل من خطأ الجهاز؛ أمر بالغ الأهمية عندما يكون خطأ أخذ العينات منخفضاً.	استخدام معدات دقيقة ومعايرة جيداً.
خطأ منهجي (تحيز)	لا يمكن تقليله بزيادة حجم العينة.	معايرة الأجهزة بانتظام.
خطأ عشوائي (ضوضاء)	يمكن تقليله عن طريق متوسط المزيد من القياسات.	استخدام معدات موثوقة وتكرار القياسات.

هل أنت مستعد لتحقيق نتائج دقيقة وموثوقة في مختبرك؟

التوازن الصحيح بين حجم العينة ودقة القياس أمر بالغ الأهمية لسلامة بياناتك. تتخصص KINTEK في معدات المختبرات عالية الدقة والمواد الاستهلاكية، وتلبي جميع احتياجات مختبرك. سواء كنت تحتاج إلى أدوات ذات دقة فائقة لمجموعات العينات الصغيرة أو معدات قوية للدراسات واسعة النطاق، فلدينا الحل لتقليل إجمالي أخطائك وزيادة الثقة في نتائجك.

اتصل بنا اليوم لمناقشة كيف يمكن لمنتجاتنا تحسين استراتيجية القياس الخاصة بك. دع خبرائنا يساعدونك في اختيار الأدوات المثالية لتطبيقك المحدد.

#نموذج_الاتصال