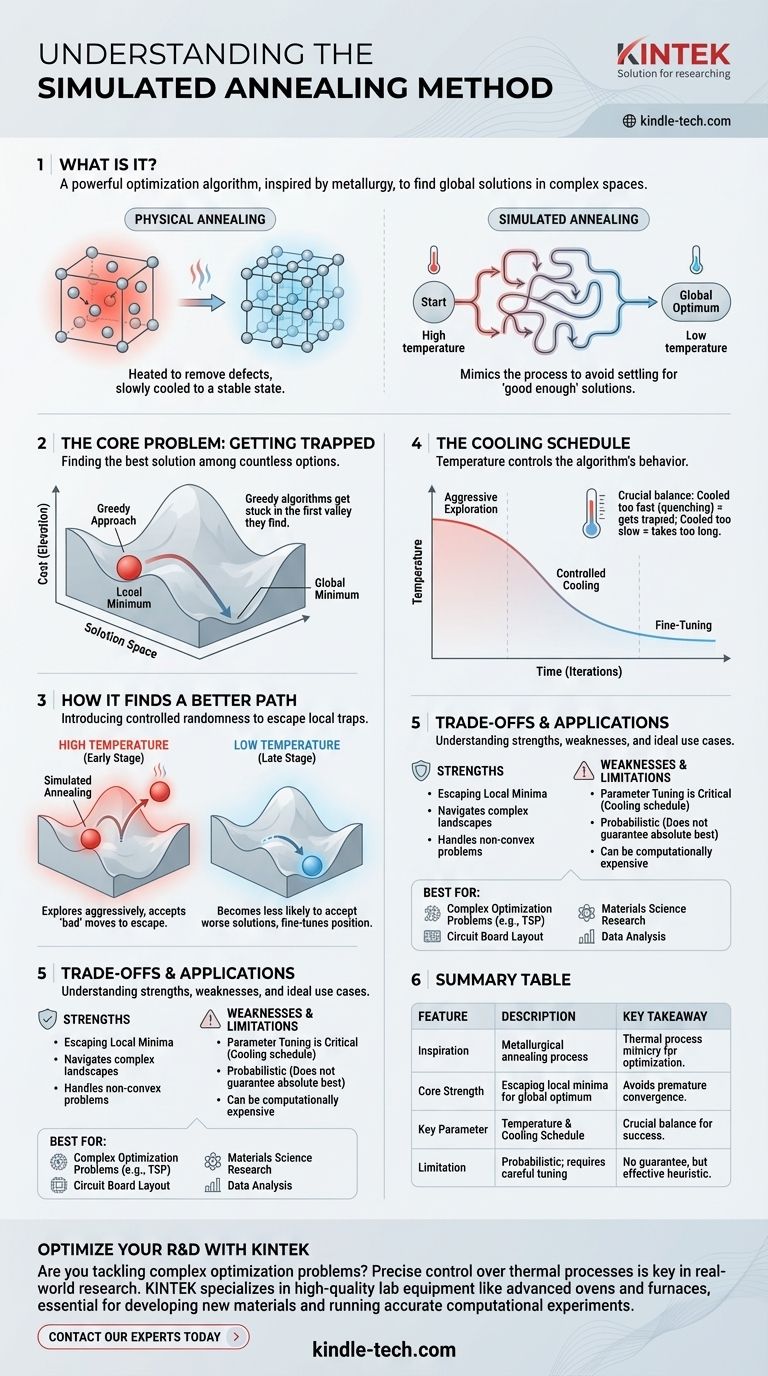
باختصار، التلدين المحاكى هو خوارزمية تحسين قوية تستخدم لإيجاد حل جيد (وغالبًا ما يكون عالميًا) في فضاء بحث واسع ومعقد. وهو مستوحى مباشرة من عملية التلدين المعدني، حيث يتم تسخين المادة ثم تبريدها ببطء لإزالة العيوب والوصول إلى حالة بلورية مستقرة ومنخفضة الطاقة. تحاكي الخوارزمية هذه العملية الفيزيائية لحل المشكلات الحسابية المجردة.
في جوهره، يتجنب التلدين المحاكى الفخ الشائع المتمثل في الاكتفاء بحل "جيد بما فيه الكفاية" من خلال محاكاة العملية الفيزيائية لتلدين المعدن. يبدأ باستكشاف مجموعة واسعة من الاحتمالات (درجة حرارة عالية) ويضيق تدريجياً تركيزه إلى حل عالي الجودة ومستقر (درجة حرارة منخفضة).
المشكلة الأساسية: الوقوع في الفخ
لفهم التلدين المحاكى، يجب عليك أولاً فهم المشكلة التي يحلها: إيجاد أفضل حل ممكن من بين عدد لا يحصى من الخيارات، وهي مهمة تُعرف باسم التحسين.
مشهد الحلول
تخيل أن كل حل ممكن لمشكلتك هو نقطة على منظر طبيعي تلالي واسع. يمثل ارتفاع كل نقطة "تكلفته" - كلما كان الارتفاع أقل، كان الحل أفضل. هدفك هو العثور على أدنى نقطة على الخريطة بأكملها، وهو الحد الأدنى العالمي.
النهج "الجشع" وعيبه
الخوارزمية البسيطة، التي تسمى غالبًا تسلق التل، ستبدأ من نقطة عشوائية وستتحرك دائمًا إلى الأسفل. هذا هو النهج "الجشع" لأنه يقبل فقط التحركات التي تحقق تحسنًا فوريًا.
المشكلة هي أن هذه الطريقة ستعلق في أول واد تجده - وهو حد أدنى محلي. ليس لديها أي طريقة لمعرفة ما إذا كان هناك واد أعمق بكثير، وهو الحد الأدنى العالمي، يقع خلف التل التالي مباشرة.
كيف يجد التلدين المحاكى مسارًا أفضل
يتغلب التلدين المحاكى على هذا القيد من خلال إدخال عنصر عشوائية متحكم فيه يسمح له بالهروب من هذه الأفخاخ المحلية.
الإلهام: التلدين الفيزيائي
في علم المعادن، يمنح تسخين المعدن ذراته طاقة كافية للحركة بحرية، مما يكسر الهياكل المعيبة وغير المثلى. عندما يبرد المعدن ببطء، يكون لدى الذرات وقت للاستقرار في شبكة بلورية قوية ومنظمة للغاية - وهي حالة من الحد الأدنى من الطاقة.
الخوارزمية: درجة الحرارة كمقبض تحكم
يتبنى التلدين المحاكى هذا المفهوم من خلال إدخال متغير درجة الحرارة. هذه ليست درجة حرارة فيزيائية، بل هي متغير يتحكم في سلوك الخوارزمية.
تبدأ الخوارزمية بدرجة حرارة عالية. في هذه الحالة، تستكشف مشهد الحلول بقوة، تمامًا مثل الذرات النشطة في المعدن الساخن. لديها احتمالية عالية لقبول التحركات التي هي أسوأ من موقعها الحالي. هذا هو المفتاح: القيام بحركة "سيئة" هو ما يسمح لها بالخروج من الحد الأدنى المحلي.
جدول التبريد
أثناء تشغيل الخوارزمية، يتم خفض درجة الحرارة تدريجياً وفقًا لـ جدول تبريد. مع انخفاض درجة الحرارة، تصبح احتمالية قبول حل أسوأ أقل وأقل.
في النهاية، عند درجة حرارة منخفضة جدًا، تتصرف الخوارزمية مثل طريقة تسلق التل البسيطة، حيث تقبل التحسينات فقط وتضبط موقعها فيما يُؤمل أن يكون الحد الأدنى العالمي.
فهم المفاضلات
مثل أي أداة قوية، التلدين المحاكى ليس حلاً شاملاً. يعد فهم حدوده أمرًا بالغ الأهمية لاستخدامه بفعالية.
القوة: الهروب من الحدود الدنيا المحلية
ميزته الأساسية هي قدرته على التنقل في المناظر الطبيعية المعقدة وغير المحدبة ذات الحدود الدنيا المحلية العديدة. بالنسبة للمشكلات التي تفشل فيها الخوارزميات الجشعة باستمرار، يعد التلدين المحاكى خيارًا ممتازًا.
نقطة الضعف: ضبط المعلمات أمر بالغ الأهمية
يعتمد أداء الخوارزمية بشكل كبير على جدول التبريد. إذا تم التبريد بسرعة كبيرة، فقد تعلق في حد أدنى محلي على أي حال ("التخميد"). إذا تم التبريد ببطء شديد، فقد يستغرق الأمر وقتًا غير عملي للعثور على حل. غالبًا ما يتطلب العثور على الجدول الصحيح التجريب.
القيد: إنها طريقة احتمالية
لا يضمن التلدين المحاكى أنه سيجد الحل الأفضل على الإطلاق (الحد الأدنى العالمي). إنها طريقة استدلالية، مما يعني أنها مصممة لإيجاد حل جيد جدًا في فترة زمنية معقولة. هناك دائمًا احتمال إحصائي بأنها تستقر في حالة دون المستوى الأمثل.
اتخاذ القرار الصحيح لمشكلتك
استخدم هذا التوجيه لتحديد ما إذا كان التلدين المحاكى هو النهج الصحيح لمهمة التحسين الخاصة بك.
- إذا كان تركيزك الأساسي هو حل مشكلة معقدة بها العديد من الأفخاخ (الحدود الدنيا المحلية): يعد التلدين المحاكى أحد أفضل الأدوات لهذه المهمة، خاصة للمشكلات الكلاسيكية مثل مشكلة البائع المتجول أو تخطيط لوحات الدوائر.
- إذا كان تركيزك الأساسي هو إيجاد حل أمثل يمكن إثباته بأقصى سرعة: يجب عليك أولاً التحقق مما إذا كانت مشكلتك بسيطة بما يكفي (على سبيل المثال، محدبة) ليتم حلها بواسطة خوارزمية حتمية أسرع مثل البرمجة الخطية أو نهج جشع قياسي.
في نهاية المطاف، يوفر التلدين المحاكى إطارًا قويًا للتنقل في مساحات البحث الشاسعة والصعبة للعثور على حلول عالية الجودة حيث تفشل الطرق الأبسط.
جدول الملخص:
| الميزة | الوصف |
|---|---|
| الإلهام | عملية التلدين المعدني (التسخين والتبريد البطيء) |
| القوة الأساسية | الهروب من الحدود الدنيا المحلية لإيجاد الأمثل العالمي |
| المعلمة الرئيسية | درجة الحرارة وجدول التبريد |
| الأفضل لـ | مشاكل التحسين المعقدة ذات العديد من الأفخاخ المحلية |
| القيد | احتمالي؛ يتطلب ضبطًا دقيقًا للمعلمات |
حسّن بحثك وتطويرك مع KINTEK
هل تتعامل مع مشاكل تحسين معقدة في علوم المواد أو الهندسة الكيميائية أو تحليل البيانات؟ تستلهم مبادئ التلدين المحاكى من العمليات الحرارية الواقعية، والتحكم الدقيق في تلك العمليات في مختبرك أمر بالغ الأهمية.
تتخصص KINTEK في معدات المختبرات عالية الجودة، بما في ذلك الأفران والمواقد المتقدمة التي توفر التسخين الموحد والتبريد المتحكم فيه الضروريين للبحث والتطوير. سواء كنت تقوم بتطوير مواد جديدة أو تشغيل تجارب حاسوبية، فإن المعدات الموثوقة هي أساس النتائج الدقيقة.
اتصل بخبرائنا اليوم للعثور على حل المختبر المثالي لتعزيز سير عمل التحسين لديك وتحقيق نتائج رائدة.
المنتجات ذات الصلة
- فرن جو الهيدروجين
- فرن تلبيد سلك التنغستن فراغ صغير
- فرن الغلاف الجوي المتحكم فيه بحزام شبكي
- 1400 ℃ فرن الغلاف الجوي المتحكم فيه
- معدات رسم طلاء نانو الماس HFCVD
يسأل الناس أيضًا
- ما هي استخدامات أفران الهيدروجين؟ تحقيق النقاء والسرعة في المعالجة بدرجات الحرارة العالية
- ما هو جو الفرن؟ دليل للتدفئة الخاضعة للرقابة للحصول على نتائج فائقة
- ما هو مثال على الغلاف الجوي المختزل؟ تعرف على كيفية تحويله للمواد في الصناعة
- ما هو استخدام فرن الغلاف الجوي؟ تحقيق معالجة حرارية دقيقة وخالية من التلوث
- متى تحتاج إلى استخدام جو متحكم فيه؟ منع التلوث والتحكم في التفاعلات
